Funktionen
Online Rechner
- Ableitungsrechner
- Integralrechner
- Exponentielles Wachstum
- Kurvendiskussion
- Quadratische Funktionen
- Konvergenz der Reihen
- Konvergenz der Folgen
- Bogenlänge
- Rotationskörper
Abstand eines Punktes von einer Ebene wird berechnet, indem der Kurzeste Weg zwischen dem Punkt und der Ebene berechnet wird. Ein Punkt kann auf einer Ebene liegen oder nicht. Im Prinzip gibt es nur 2 Lagen von einem Punkt und einer Ebene zueinander. Der Abstand eines Punkts im Raum zu einer Ebene wird in der Regel so ermittelt, dass vom Punkt aus eine Gerade zur Ebene gezogen wird. Diese Gerade muss zum Normalvektor der Ebene Parallel sein, da der Normalvektor immer senkrecht zur Ebene steht und der Abtand auch immer senkrecht sein muss, da eine senkrechte Strecke als Abstand (kürzester Weg) gilt. Anschließend wird die Gerade die Ebene an einer Stelle schneiden. Der Abstand zwischen dem AUsgangspunkt zu dem Schnittpunkt ist der Abstand zwischen dem Punkt und der Ebene. Daraus resultierend wird eine Formel auch dafür aufgestellt, die für diesen Online-Rechner auch genutzt wurde. Gebe die Pinktkoordinaten und auch die Ebenengleichung in Parameterform an. ax+by+cz=d
P=
X1
Y1
Z1
E :
X1 +
Y1 +
Z1 =
Die Lage zweier Ebenen kann entweder sich schneidend oder Parallel sein. Es gibt keine dritte Variante.
Ebenen sind Parallel, wenn die Normalvektoren beider Ebenen vielfache voneinander sind.
Parallele Ebenen können identisch sein, wenn der Abstand null bzw. mindestens ein gemeinsamer Punkt
vorhanden ist.
Ebenen schneiden sich, wenn die obige Bedingung nicht erfüllt ist. Also wenn die Normalvektoren keine Vielfache sind.
Durch einen Schnitt von Ebenen entsteht eine Gerade, die auf beiden Ebenen liegt. Diese nennt sich die Schnittgerade.
Schnittgeraden haben Richtungsvektoren, die Senkrecht zu beiden Normalvektoren verlaufen.
Anhand dieser Information lässt sich der Richtungvektor der Schnittgeraden durch das Kreuzprodukt von beiden Normalvektoren
berechnen. Unten kannst du die Ebenengleichungen angeben, um die Schnittgeradengleichung zu erhalten.
E1 :
X +
Y +
Z +
= 0
E2 :
X +
Y +
Z +
= 0
Abstand zwischen zwei Punkten lässt sich leicht anhand einer Formel ausrechnen.
Die Formel ist durch eine Erweiterung von Satz des Pythagoras im Raum entsdanden.
P1=
x1
| x2
| x3
P2=
x4
| X5
| x6
Koordinatenform
Parameterform
x +
y+
z+
=0
Parameterform
X =
+ r .
+ s .
X =
+ r .
+ s .
X =
+ r .
+ s .
Koordinaten der 3 Eckpunkte
x1
| y1
| z1
x2
| y2
| z2
x3
| y3
| z3
a
d
b
X
c
ir
x +
= 0
x +
y +
= 0
x +
y +
= 0
f(x)
x +
y +
z +
= 0
x +
y +
z +
= 0
x +
y +
z +
= 0
Der Stochastikrechner berechnet die Werte zu stochastischen Prozessen.
Der Fixvektor bzw. die stablie Verteilung lässt sich ausrechnen, indem die Periodenzahl als eine große Zahl angenommen wird.
Wenn die Ergebnisse beim Variieren der t-Werte nicht abweichen, ist der Ergebnisvektor der stabile Vektor.
Übergangsmatrix
X
Verteilungsvektor
=
Periodenanzahl=
n =
k =
Hier kann deine Folge als eine Funktion eingegeben und den Anfangswert der Folge bestimmt werden.
Der Folgenrechner berechnet im Augenblick den Grenzwert der Folge im Falle einer Konvergenz.
x =
f(x)
Nur eine Ebene verläuft durch 3 Punkte, die nicht auf einer Geraden liegen. Mithilfe der 3 Punkte
lassen sich 2 Vektoren aufstellen, die die Richtungsvektoren der Ebene bilden können. Der gemeinsame Punkt
beider Vektoren kann als Ortsvektor bzw. Spannvektor betrachtet werden.
Entsprechend der obigen Erläuterung wird die Ebenengleichung aufgestellt und angezeigt, nachdem doie Koordinaten der
3 Punkte eingegeben worden sind. Dieser Online-Rechner gehört zu Ebenenrechnern, die zur Aufstellung einer Ebenengleichung
in Koordinatenform dient. Wenn die Parameterform der Ebenengleichung erwünscht ist, kann dies durch den
anderen Online-Rechner (Umformen der Ebenengleichungen) erzielt werden.
A =
B =
C =
Mit dem Online-Rechner Binomialkoeffizient kannst du anhand von deiner Eingaben (n und k) den Binomialkoeffizient berechnen lassen.
Der Binomialkoeffizient-Rechner wird berechnet, indem n! durch (k!*(n-k)!) dividiert wird.
X =
+ r .
X =
+ r .
X =
+ r .
X =
+ s .
X =
+ r .
+ r .
Der Online-Rechner Binomialverteilungsrechner bzw binomcdf-Rechner und oder binompdf-Rechner bietet
die Ermittlung der Wahrscheinlichkeit einer
Verteilung an, die der bernulli-Kette entspricht. Dabei handelt es sich um ja oder nein, falsch oder richtig,
gesund oder krank. Wenn solche Form von Aufgaben auftreten, kommt die binomialverteilung direkt im Vorschein.
Diese Aufgaben lassen sich von unserem Online-Rechner leicht lösen, indem du die untenstehenden Felder ausfüllst.
n ist die gesamte zu beobachtende Zahl,
k ist die ausgesuchte Menge und p ist die zu erwartende Wahrscheinlichkeit (Erwartungswert) bei der Aufgabenbedingung,
die der Ausgesuchten zugewiesen ist.
Lass die Wahrscheinlichkeit von unserem Online-Rechner ermittlen.
Beim Lösen deiner Aufgabe wird dir die Binomcdf auch direkt angezeigt. Diese entspricht der Summe
aller Wahrscheinlichkeitbeträgen ab x=0 bis x=k. Also binomcdf: F(n,p,k)= P(x<=k).
Das obige Ergebnis entspricht aber der Punktwahrscheinlichkeit an x=k. Also binompdf: B(n,p,k) = P(x=k)
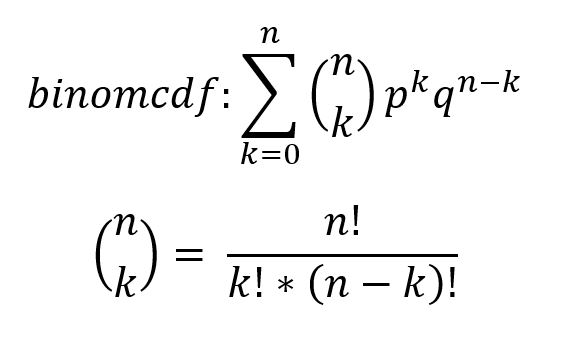
An welchem Wochentag bin ich geboren? Möchtest du wissen, an welchem Wochentag du geboren bist? Du kannst dein Geburstdatum bei unserem Tagerechner eingeben und das Ergebnis aufrufen. Wenn du wissen möchtest, an welchem Wochentag z.B dein Hochzeitstag, Verlobungsdatum oder ein bestimmtes geschichtliches Ereignis war, kannst du den Tagerechner nutzen.
Mit unserem Wasserrechner erfährst du, wie viel Wasser (reines Wasser) du bisher in deinem Leben getrunken hast. Hierfür musst du vier Daten angeben:
-Geburtsdatum
-heutiges Datum
-Wie oft du in der Regel Wasser trinkst
-Gewicht während der Pubertät
-heutiges Gewicht
Anschließend erhältst du dein Ergebnis in zwei Formaten:
* Getrunkene Wassermenge in Liter
* Das getrunkene Wasservolumen in Form eines würfelförmigen Pools
Wie viel Wasser trinkst du in der Regel? (wenig, normal, viel)?
 Anfangsdatum
Anfangsdatum
Mit dem Fibonacci-Rechner kannst du die Fibonacci-Zahlen generieren lassen. Die Eingabe ist dabei "n". Als Ergebnis werden sowohl die n-te Zahl als auch die Division (das Verhältnis) zwischen der Zahl und der vorherigen Zahl angezeigt. Man sieht, dass dieses Verhältnis bei Fibonacci-Zahlen auf ca. 1,618 konvergiert.
Beispiel: Die zweite Fibonacci-Zahl ist 1 und die Dritte ist 2. Wenn die 4. Zahl aufzurufen ist, muss bei dem Eingabefeld die Zahl 4 eingegeben werden. Danach erscheint die 4. Zahl, die aus der Summe von 1 und 2 entsteht. Also 3.
Das Verhältnis dabei ist 3 dividiert durch 2. Also 1,5.
Mit dem Rechner "exponentielles Wachstum" kann man die Wachstums- bzw. Zerfallsaufgaben rechnen lassen. Dafür sind 3 Daten erforderlich.
- Anfangswert (a)
- Wachstumsrate oder Zerfallsrate.
Hinweis: Im Falle eines Zerfalls (Abnahme) ist b kleiner als 1 und bei einer Zunahme (Wachstum) ist diese größer als 1.
- Zeit oder die erreichte Menge nach einer Zeit (t). Also f(t).
Hinweis: Alle 4 Felder dürfen nicht belegt werden. Als Ergebnis erhältst du auch die erste Ableitung der aufgestellten Wachstumsfunktion in Form von f'(x)
Mit dem Rechner "Kurvensiskussion-Rechner" für die Funktionen dritten Grades kann die Funktion eingegeben werden, indem die Faktoren der Funktion als a,b,c und d eingegeben werden. In einem Augenblick werden Nullstellen, Extrempunkte (Hochpunkt und Tiefpunkt), und der Wendepunkt angezeigt. Die Nullstellen einer Funktion 3. Grades kann entweder numerisch oder durch Formeln ermittelt werden. Wenn sogar nur eine Lösung gefunden wird, können die anderen ggf. Lösungen anhand von einer Division der Funktion durch einen Term, der aus der ersten Lösung besteht (x-x1), berechnet werden. Da das Ergebis der oben genannten Division ein quadratischer Term ist, können die nächsten Lösungen anhand von der pq-Formel oder andere bekannte Formel ausgerechnet werden.
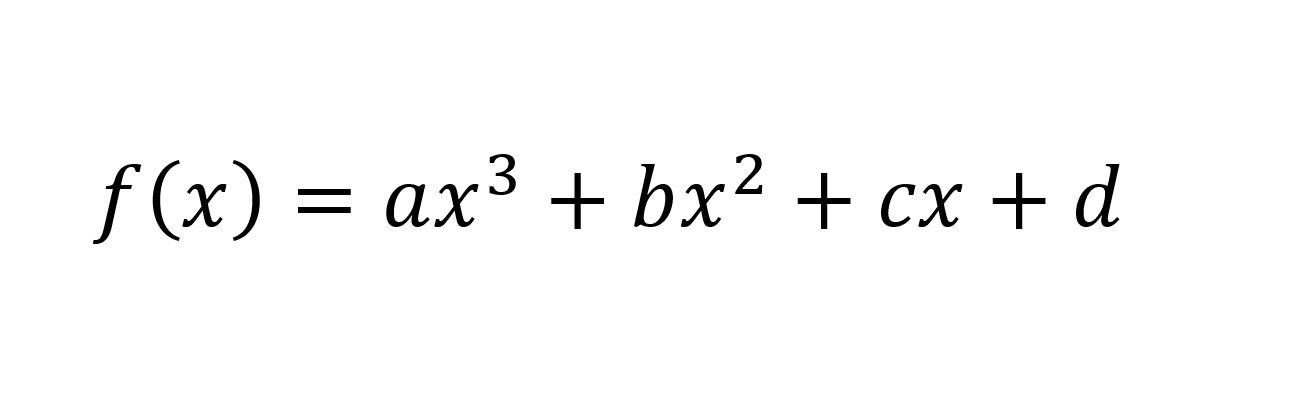
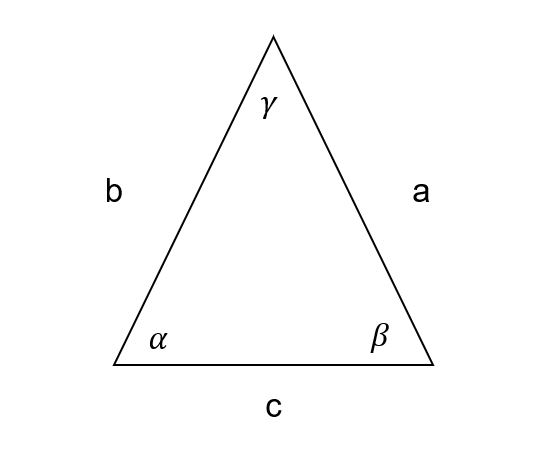
Mit dem Dreieck-Rechner kann man mehrere Winkelberechnungen und Seitenberechnungen
durchführen lassen.
Außerdem wird der Flächeninhalt des Dreiecks auch berechnet und mit anderen Ergebnissen angezeigt.
Wenn alle Seitenlängen vorhanden sind, musst du a,b und c ausfüllen und alle anderen Felder leer lassen.
Ist eine Seite und 2 Winkel gegeben, muss die bestehende Seite als a und die Winkel als alpha
und beta eingegeben werden.
Wenn ein Winkel und 2 Seiten vorliegen, sollten a, b und gamma ausgefüllt werden.
Mögliche Eingaben:
1: a, b, c
2: a, b, gamma
3: a, alpha, beta
Mögliche Eingaben:
1: a, b, c
2: a, b, gamma
3: a, alpha, beta

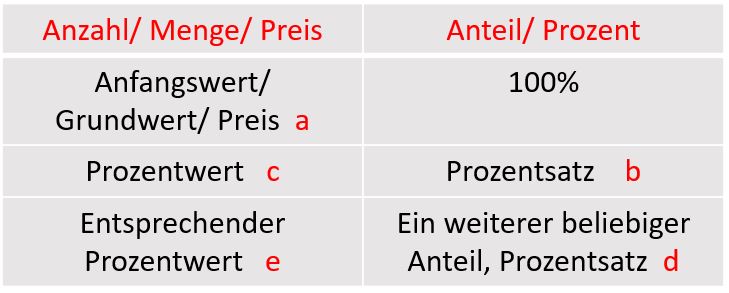
Mit dem Prozent-Rechner können mehrere unbekannte Variablen ausgerechnet werden. Wenn der Anfangswert und der Prozentsatz bekannt
sind, kann der Prozentwert ausgerechnet und angezeigt werden. Beim Vorliegen von 2 Prozentwerten und einem Prozentsatz oder Sinzsatz
wird der unbekannte Prozentsatz bzw. Zinssatz gerechnet. Im Gegenzug sollten 2 Prozentsätze bzw. Anteile und ein Prozentwert
existieren, wird der andere Prozentwert errechnet.
Probiere den Prozentrechner aus.
Mögliche Eingaben:
1: a, b
2: a, c
3: b, c
4: b, c, d
5: e, b, c
Mögliche Eingaben:
1: a, b
2: a, c
3: b, c
4: b, c, d
5: e, b, c
Mit dem Rechner "Quadratische Funktionen" für die Funktionen zweiten Grades kann die Funktion eingegeben werden, indem die Faktoren der Funktion als a,b,c und d eingegeben werden. In einem Augenblick werden Nullstellen, Scheitelpunkt (Hochpunkt und Tiefpunkt), und die Funktionsgleichung in Scheitelpunktform aufgestellt. Die binomischen Formel werden hier genutzt, um die quadratische Ergänzung durchzuführen. Die ersten binomischen Formel bildet einen quadratischen Term und einen zusätslichen Term. Diese nennt sich die quadratische Ergänzung, anhanddessen die quadratische Gleichung in Scheitelpunktsform erstellt wird.Beispielsweise bei 2x^2-3x+2 wollen wir jetzt anhand von der ersten binomischen Formel die Gleichung bzw die Funktion in Scheitelpunktform umwandeln. Dafür gib bitte für a=2, b=-3 und für c=2 ein. Da erhätst du in einem Augenblick die Lösungen und die Scheitelpunktform.
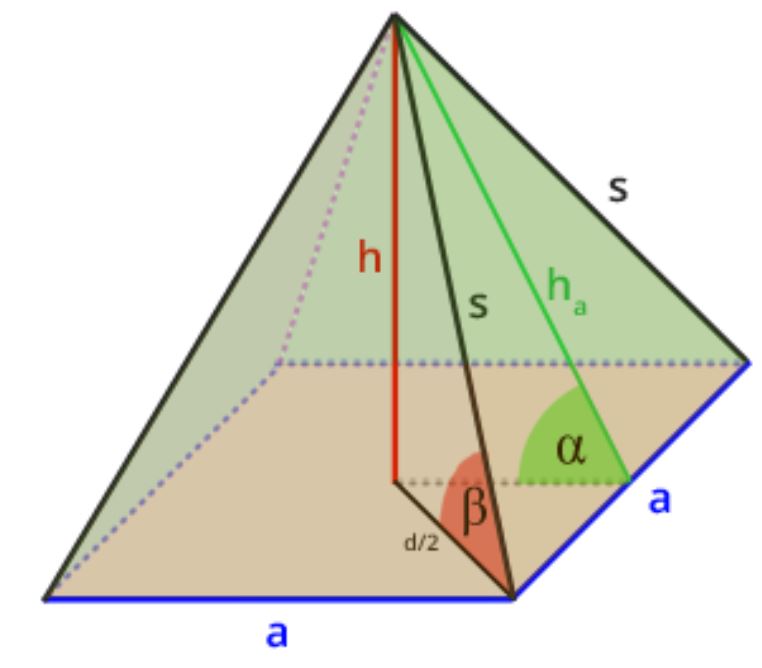
Mit dem Pyramidenrechner können alle unbekannten Größen einer Pyramide anhand von nur 2 Eingaben bestimmt werden.
Folgende Felder sind vorgesehen: Seitenlänge der Grundfläche (Viereck),Höhe der Pyramide, Höhe der Wände (Dreieck), Länge der Schenkel
der Dreiecken. Wenn nur 2 Parameter eingegeben werden, erhältst du anhand vom Pyramidenrechner alle weiteren Variablen
ausgerechnet mit dem Volumen, Oberflächen- und Mantelflächeninhalt.
Mögliche Eingaben:
1: a, h1
2: a, h2
3: a, s
4: h2, s
Mögliche Eingaben:
1: a, h1
2: a, h2
3: a, s
4: h2, s
Mit Bogenläge Rechner bzw. Kurvenlänge Rechner kannst du die Länge einer
Kurve einer Funktion in einem bestimmten Intervall ausrechnen lassen.
Das Ergebnis wird Näherungsweise und durch numerische Berechnungen anhand der folgenden Formel
ausgerechnet und angezeigt. Die Bogenlänge kann durch das Summieren aller sehr kleinen Strecken auf
der Kurve berechnet werden, die mittels Aufteilung der Kurve und mehrerer Punkte auf dem Graphen
entsanden sind. Wenn das Intervall diskretisiert und aufgeteilt wird, entstehen mehrere Punkte
entsprechend der erstellten x-Werte im Intervall. Wenn 2 nebenstehende Punkte miteinander verbunden werden,
entstehen neue kleine Strecken, die mit Satz des Pythagoras zu bestimmen sind. Durch das Integral kann die
Summe aller Streckenlängen als Bogenlänge angegeben werden.
Bestimme das Intervall von a nach b. Gib die Funktionsgleichung der Kurve wie im Beispiel ins Feld ein.
Genieße unseren Bogenlänge Rechner.
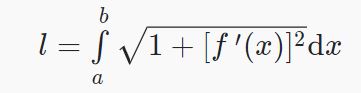
a =
b =
f(x)
Der Rotaionskörper ist ein Teil einer Kurve, der um eine Gerade oder Achse rotiert, sodass ein
Körper symmetrisch zur Rotationsachse entsteht. In diesem Rechner also Ratationskörper Rechner wird eine Rotation um
die x-Achse berücksichtigt.
Das Volumen dieses Körpers lässt sich anhand von Integralrechnungen näherungsweise berechnen. Das Volumen sieht ähnlich wie ein
Kegel, bei deem dies durch die Berechnung des Umfangs der Grundfläche mal die Höhe berechnet wird. In diesem Falle besteht auch der
Körper aus mehreren sehr dünnen (h->0 ist die Dicke) Zylindern. Das Volumen aller Zylinder werden aufsummiert und als ein Integral aufgestellt.
Dies wird in unserem Rotationskörper Rechner numerisch ausgerechnet und angezeigt.
Die Mantelfläche lässt sich auch anhand von einem Integral berechnen, sodass mehrere dünne Kegelstümpfe mit einer Länge von einem Teil der
Kurvenlänge ( hier. ) und den effektiven Radius direkt in der Mitte jedes Kegelteils wie folgt berechnet wird: Kurvenlänge * Summe
aller in der Mitte stehenden Radien * 2 * Pi, da die jeweiligen Umfänge zu berechnen sind.
Die Mantelfläche wird auch in unserem Rotationskörper Rechner automatische ausgerechnet und angezeigt.
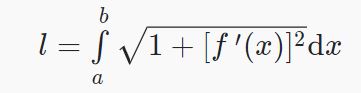
a =
b =
f(x)



